Causal Model information
- Model Approach: Causal Model Notebook
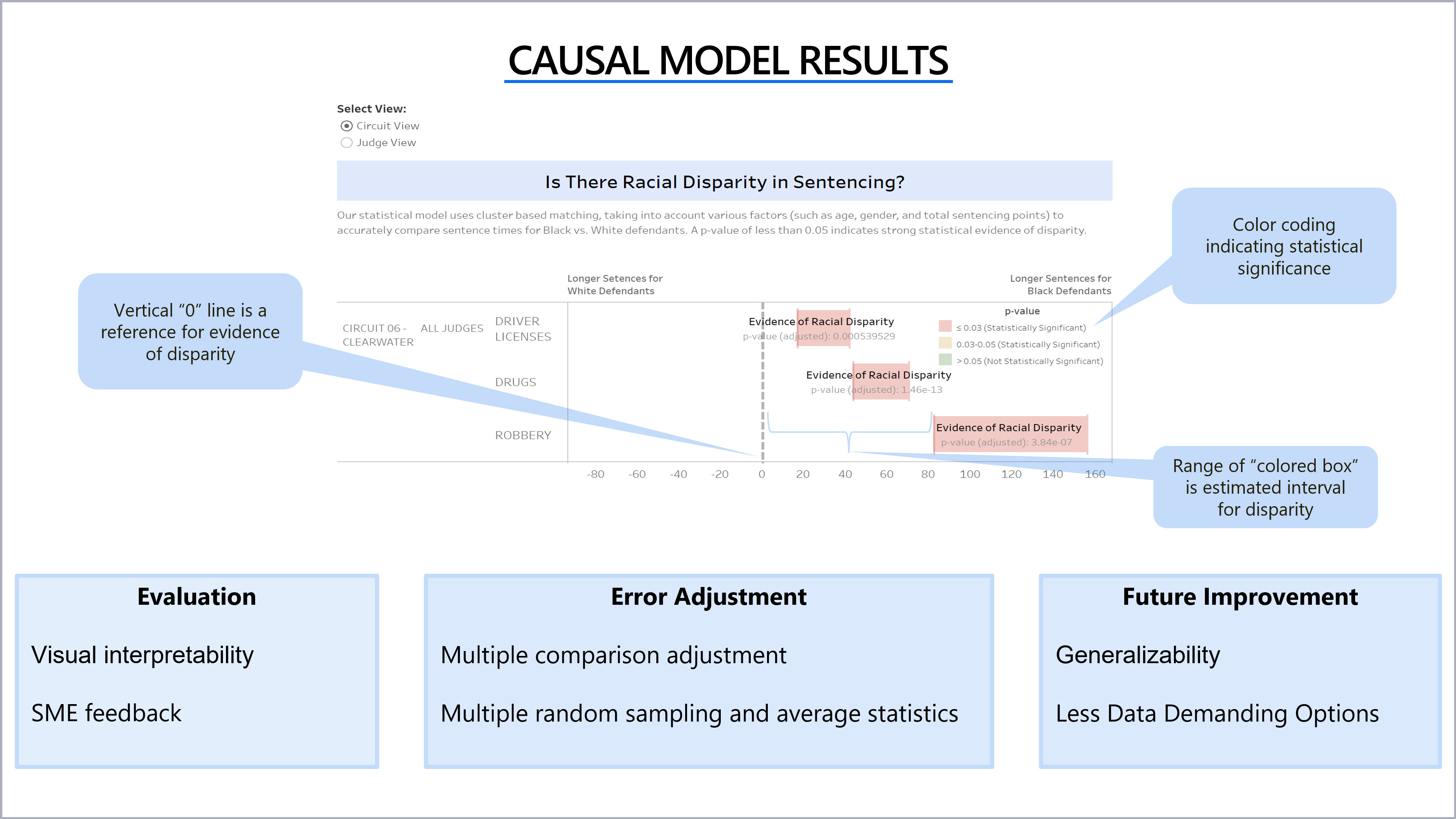
- Circuits Used: CIRCUIT 06 - CLEARWATER, CIRCUIT 11 - MIAMI, CIRCUIT 17 - FT. LAUDERDALE
- Crime Types Used: Drugs, Robbery, Burglary, Drivers Licenses
- List of judges used: Florida Sentencing Details by Judge
Datasets Used
Number of Years in Dataset
Data Science Techniques Applied
Subject Matter Experts Involved
The Use of Judge Name as a Segment in our Predictive and Causal Models
Due to direct feedback from our subject matter experts, the predictive and causal modelling approaches have been run with and without judge information for comparison reasons.
We chose counties with enough judge information for our modelling purposes and noted that many of the judges names we misspelled, shortened or abbreviated. We have applied "fuzzy" search logic, which you can find in this notebook, to group these variations in judges names together.
The Use of Segments for the Predictive and Causal Models
To narrow the scope for our MVP we segmented the three circuits and three crime types listed below
- Circuits: CIRCUIT 06 - CLEARWATER, CIRCUIT 11 - MIAMI, CIRCUIT 17 - FT. LAUDERDALE
- Crime Type: Drugs, Robbery and Traffic Control
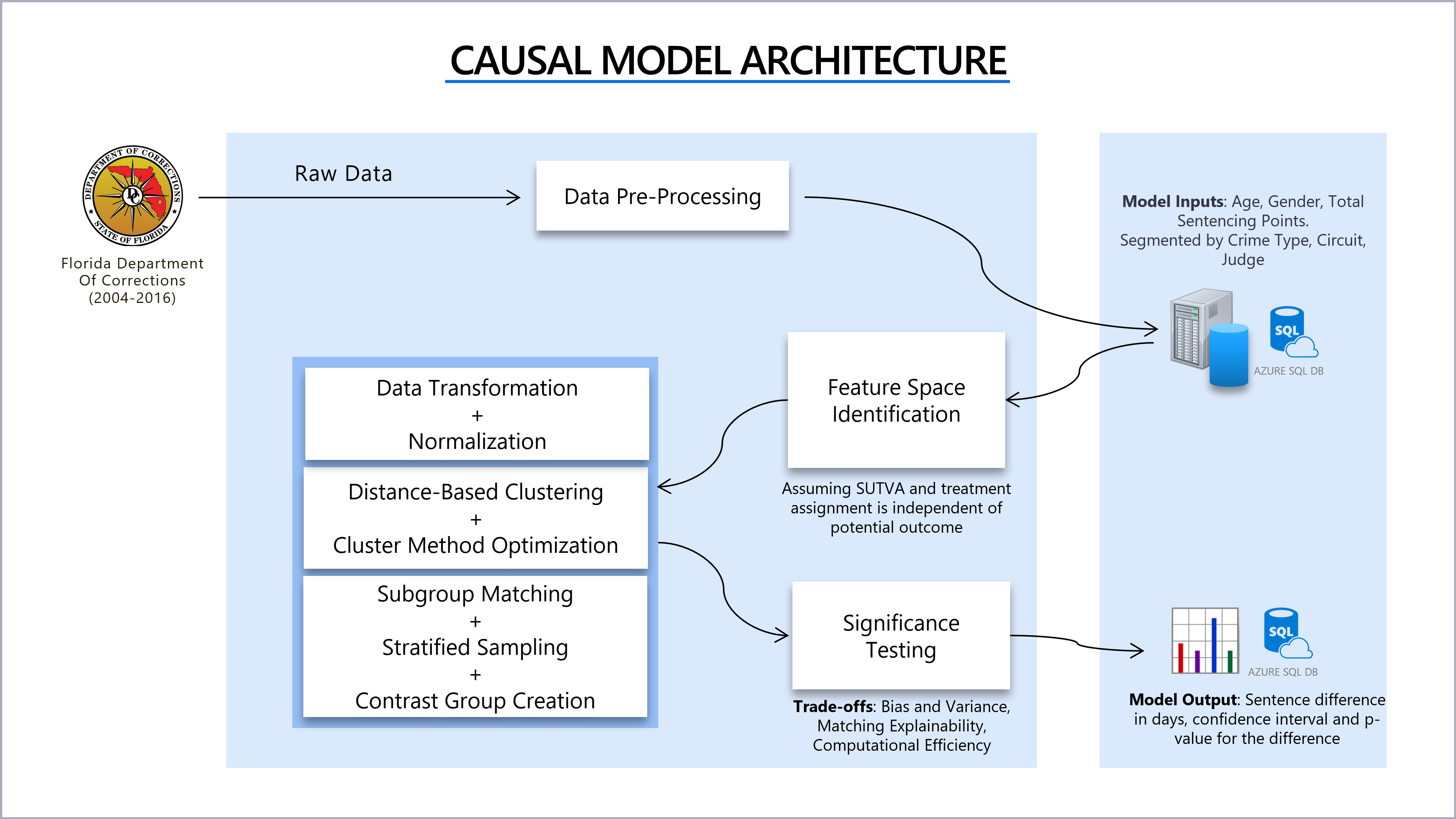
Causal Modelling:
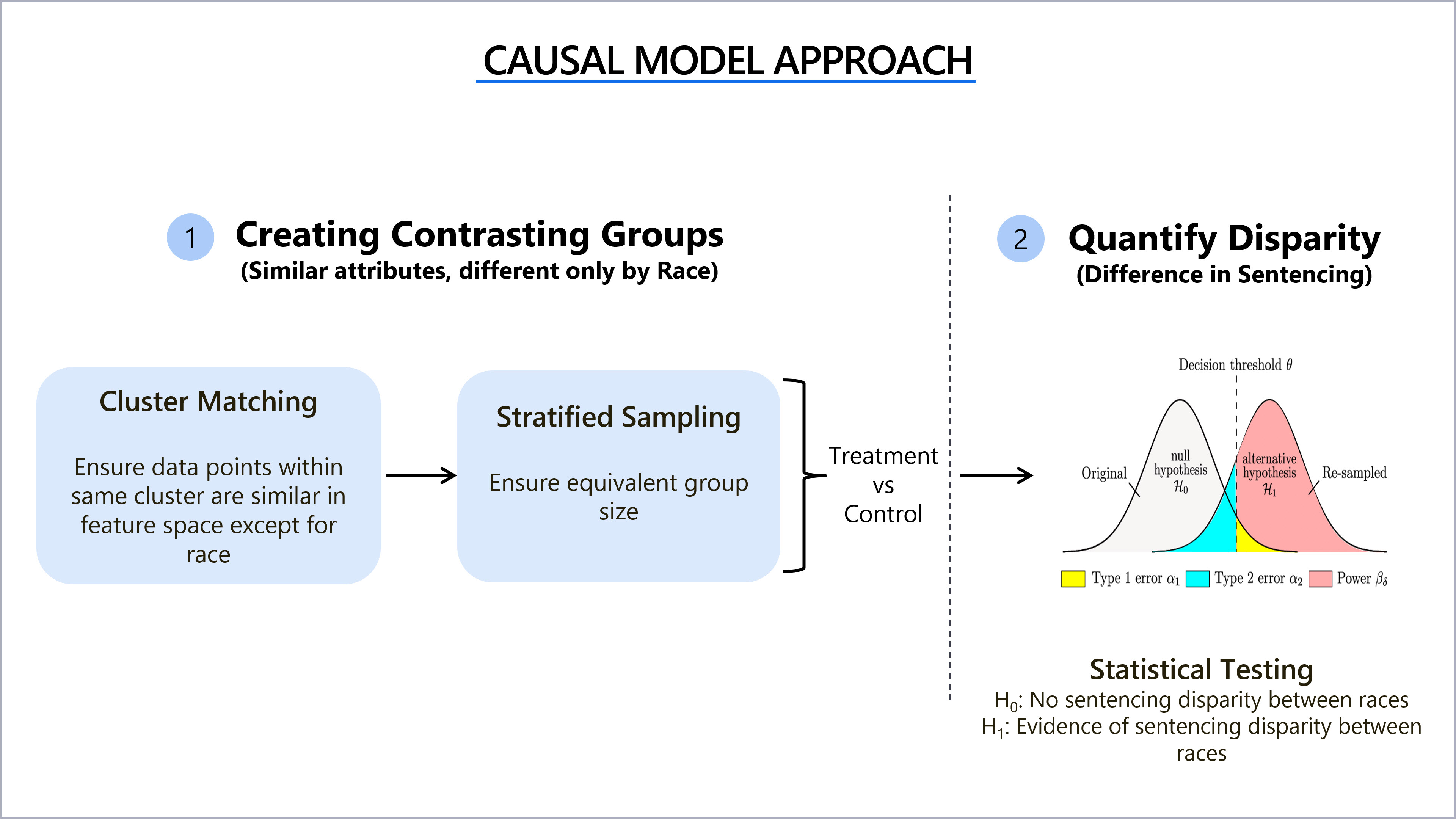
For causal modelling we focused on robustness and applicability through a Quasi-experimental design using matching methods.
- Generate data clusters based on feature proximity determined through k-means and cosine similarity on gender, age and total sentencing points
- Clusters are generated using distance based clustering (Good explainability)
- Clustering based matching is less situational than many other matching methods
- Age: 20-86 years of age
- Gender: M/F
- Total Points: Number of points for the defendent
- Stable unit treatment value assumption (SUTVA): Treatment of one unit does not affect the potential outcome of other units
- Ignorability: Treatment assignment is independent of the potential outcome
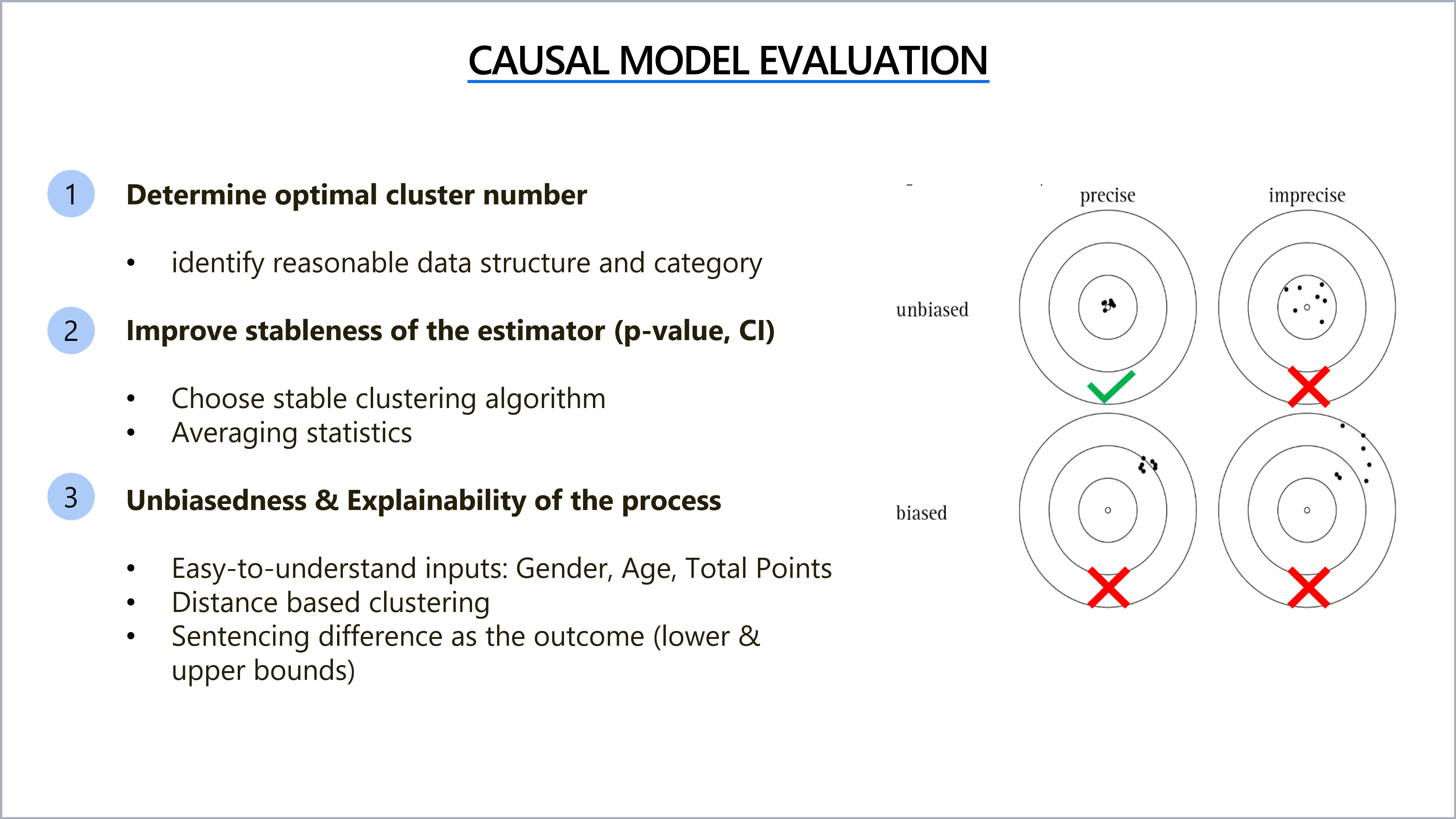
- Clustering:
- Elbow method
- Intra cluster variance
- Sensitivity Analysis
- Confidence Interval and Significance test evaluation
- Bias and Variance
- Matching Explainability
- Computation Efficiency